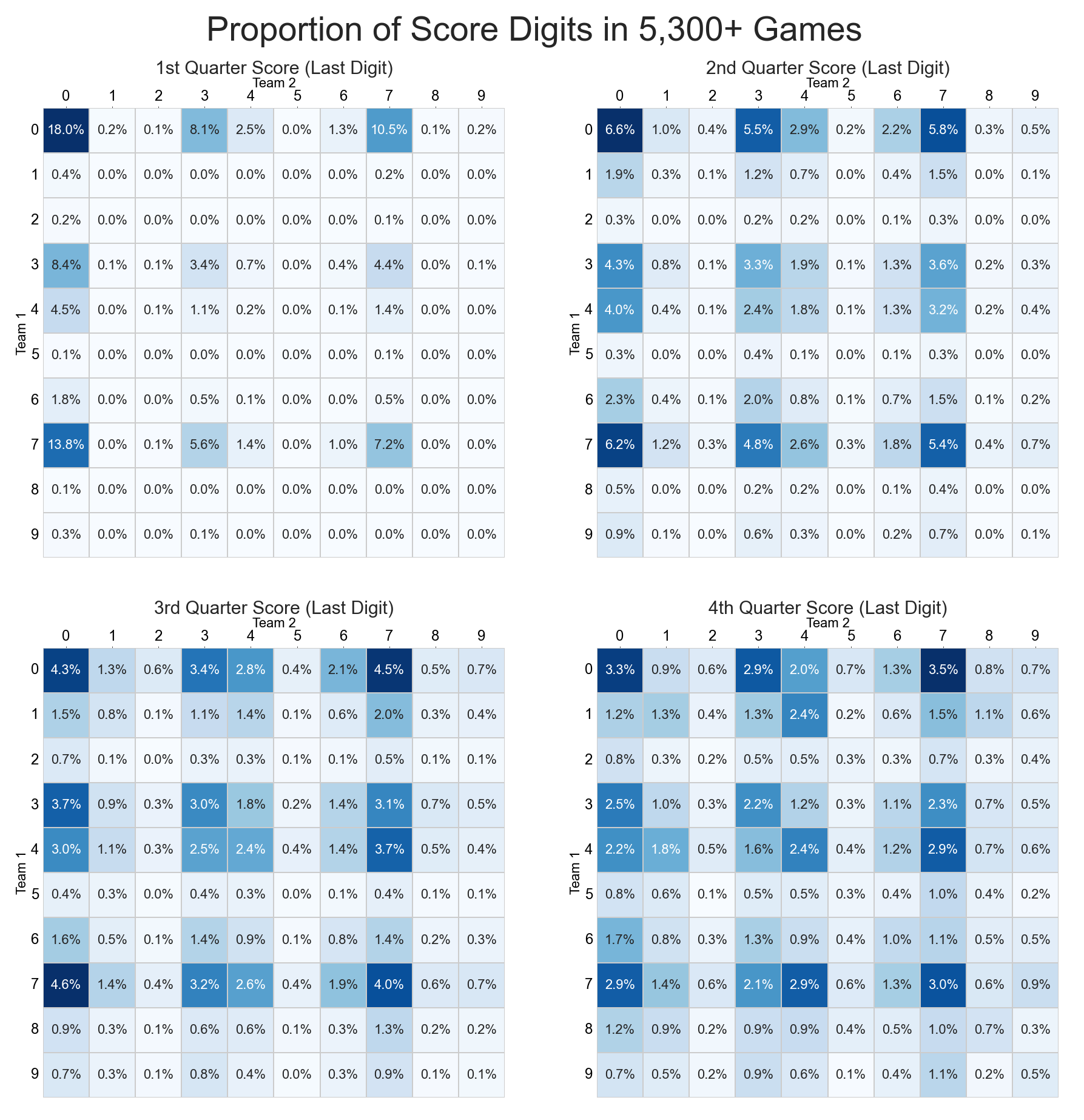
The heat maps are formatted just like the grid of the Super Bowl pool. Inside each square, we have the percentage of our 5,300+ games whose quarters ended with that digit pair. And in true heat map fashion, the darker the square, the more often that digit pair came up. We can clearly see hot spots at the intersections of 0, 7 and 3 at the start of the game, and those squares stay the darkest throughout the whole game.
If we add up the percentages, we can truly get a good understanding for how valuable the 0 and 7 pairings are, especially early in the game. Nearly 50% of all 5,359 games ended their first quarter with some pairing of 0s and 7s. If history is to be repeated, and you have some variation of 0 and 7 in your pool, you’ve got about a 50% chance of making money after the first quarter on Sunday. Lucky you!
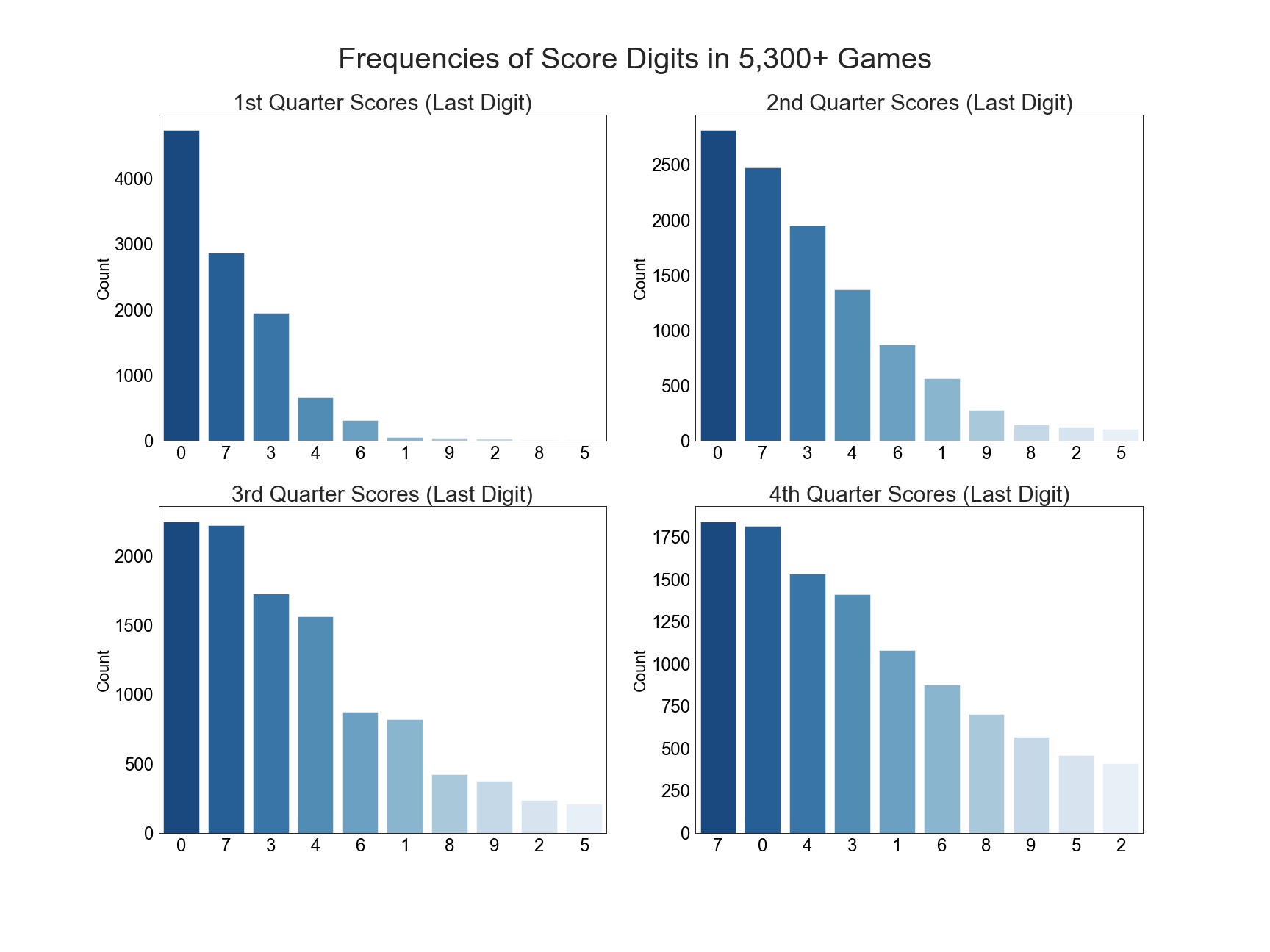
Just like with the bar charts, we can see some of the 3, 4, 6, and 1 squares becoming darker as the game continues. Overall, the percentages even out considerably by the fourth quarter. In the first quarter, the best square won around 18% of the time, but by the end of the game, the best squares are winning around 3% of the time. So it would seem like the playing field has become much more level, right?
Not necessarily. The best squares are still the 0s and 7s, followed closely by 3s and 4s, and then the 6s and 1s. Did you notice what squares never really seem to get dark? Yup, our old friends 2, 5, 8 and 9. To be fair, the 8 and 9 squares have some color by the fourth quarter, and some of the squares pairs even break a 1% success rate!!! But the 2 and 5 squares are about as pale as a certain data analyst with a blog he updates sporadically. If we look back to the bar charts, we can see that 2 and 5 are essentially the worst digits to have in a pairing. They have a lower frequency than nearly every other digit for pretty much the entirety of any game. So even if one of your digits is a valuable 7 or 0, if the other is a 2 or 5 , your chances drop considerably!
Shall we really dive in to the misery of 2 and 5? What happens if you have both a 2 and a 5? What if you were very bad in a past life and your digit pair is either (2,5) or (5,2)? If that’s your situation, you’re looking at somewhere between a 0.1% – 0.4% chance of making any money at all for the entire game. Over all four quarters, those pairings have been successful less than half a percent of the time! Your best case scenario for a 2 and 5 pairing means you have a 99.6% chance of losing.